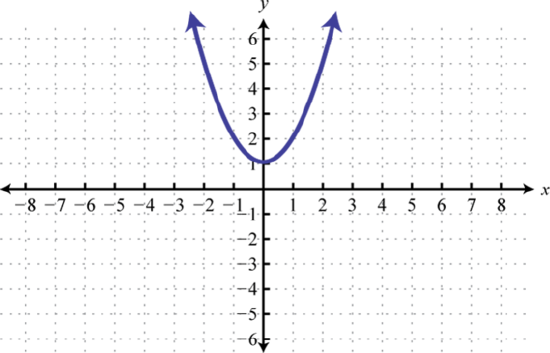
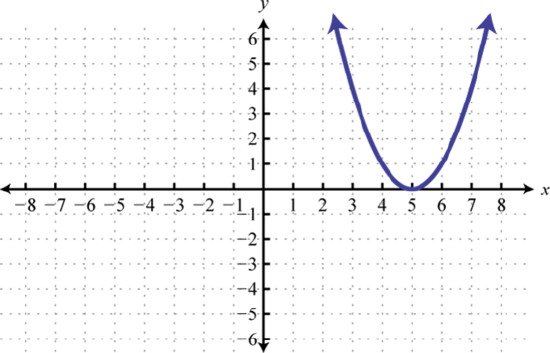
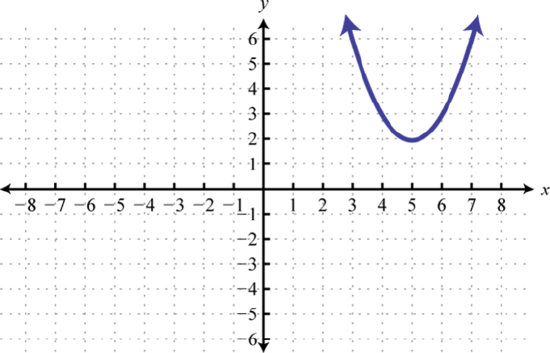
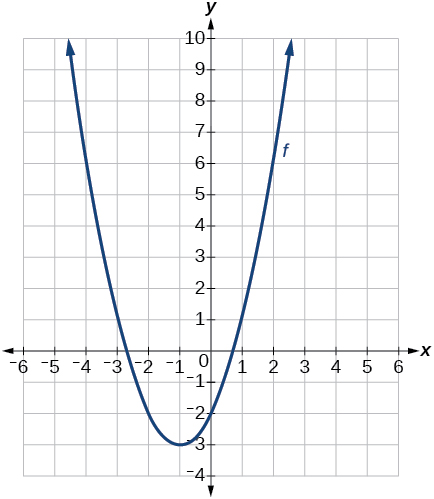
\(f(t)=(t+1)^2−3\)
Answers to Odd Exercises: 7. The graph of \(f(x+43)\) is a horizontal shift to the left \(43\) units of the graph of \(f\). 9. The graph of \(f(x-4)\) is a horizontal shift to the right \(4\) units of the graph of \(f\). 11. The graph of \(f(x)+8\) is a vertical shift up \(8\) units of the graph of \(f\). 13. The graph of \(f(x)−7\) is a vertical shift down \(7\) units of the graph of \(f\). 15. The graph of \(f(x+4)−1\) is a horizontal shift left \(4\) units and vertical shift down \(1\) unit of the graph of \(f\). 17. The graph of \(g\) is a vertical reflection (across the x-axis) of the graph of \(f\). 19. The graph of \(g\) is a vertical stretch by a factor of 4 of the graph of \(f\). 21. The graph of \(g\) is a horizontal compression by a factor of \(\frac\) of the graph of \(f\). 23. The graph of \(g\) is a horizontal stretch by a factor of 3 of the graph of \(f\). 25. The graph of \(g\) is a horizontal reflection across the y-axis and a vertical stretch by a factor of 3 of the graph of \(f\).
Exercise \(\PageIndex
| 27. \(g(x) = x^ + 1\) 28. \(g(x) = x^ − 4\) 29. \(g(x) = (x − 5)^\) 30. \(g(x) = (x + 1)^\) | 31. \(g(x) = (x − 5)^ + 2\) 32. \(g(x) = (x + 2)^ − 5\) 33. \(f(t)=(t+1)^2−3\) 34. \(f ( x ) = - ( x + 2 ) ^ < 2 >\) | 35. \(f ( x ) = - x ^ < 2 >+ 6\) 36. \(g ( x ) = - 2 x ^ < 2 >\) 37. \(g(x)=4(x+1)^2−5\) 38. \(g(x)=5(x+3)^2−2\) | 39. \(h ( x ) = \tfrac < 1 > < 2 >( x - 1 ) ^ < 2 >\) 40. \(h ( x ) = \tfrac < 1 > < 3 >( x + 2 ) ^ < 2 >\) 41. \(f ( x ) = ( -\tfracx - 3 ) ^ 2 + 1\) 42. \(g(x)=(-2x+3)^2 -4 \) |
\( \bigstar\) Begin by graphing the square root function \(f(x)=\sqrt\). State the transformations needed to apply to \(f\) to graph the function below. Then use transformations to graph the function.
| 43. \(g(x) = \sqrt − 5\) 44. \(g(x) = \sqrt\) 45. \(g(x) = \sqrt + 1\) 46. \(g(x) = \sqrt + 3\) | 47. \(a(x)=\sqrt\) 48. \(m(t)=3-\sqrt\) 49. \(h ( x ) = \sqrt < - x >+ 2\) 50. \(g ( x ) = - \sqrt < x >+ 2\) | 51. \(g ( x ) = - \frac < 1 > < 2 >\sqrt < x - 3 >\) 52. \(h ( x ) = - \sqrt < x - 2 >+ 1\) 53. \(f ( x ) = 4 \sqrt < x - 1 >+ 2\) 54. \(f ( x ) = - 5 \sqrt < x + 2 >\) | 55. \(k(x) = \sqrt - 1\) 56.1 \(a(x) = \sqrt x - 4> \) 56.2 \(b(x) = \sqrt+2 \) |
\( \bigstar\) Begin by graphing the absolute value function \(f(x)=| x |\). State the transformations needed to apply to \(f\) to graph the function below. Then use transformations to graph the function.
| 57. \(h(x) = |x + 4|\) 58. \(h(x) = |x − 4|\) 59. \(h(x) = |x − 1| − 3\) 60. \(h(x) = |x + 2| − 5\) | 61. \(g ( x ) = - | x - 1 |\) 62. \(h(x)=|x−1|+4\) 63. \(f ( x ) = - 3 | x |\) 64. \(f ( x ) = - | x | - 3\) | 65. \(h(x)=−2|x−4|+3\) 66. \(n(x)=\dfrac|x−2|\) | 67. \(h ( x ) = | - 3 x + 4 | - 2\) 68. \(g(x) = | \tfracx-2| + 1 \) |
\( \bigstar\) Begin by graphing the standard cubic function \(f(x) = x^3 \). State the transformations needed to apply to \(f\) to graph the function below. Then use transformations to graph the function.
| 69. \(h(x) = (x − 2)^\) 70. \(h(x) = x^ + 4\) 71. \(h(x) = (x − 1)^ − 4\) | 72. \(h(x) = (x + 1)^ + 3\) 73. \(g ( x ) = - ( x + 2 ) ^ < 3 >\) 74. \(k(x)=(x−2)^3−1\) | 75. \(g ( x ) = - x ^ < 3 >+ 4\) 76. \(m(x)=\tfracx^3\) 77. \(g ( x ) = - \frac < 1 > < 4 >( x + 3 ) ^ < 3 >- 1\) | 78. \(q(x)=\big(\tfracx\big)^3+1\) 79. \(p(x)=\big(\tfracx\big)^3−3\) |
\( \bigstar\) Begin by graphing the appropriate parent function : the basic cube root function \(f(x)=\sqrt[3]\), constant function \(f(x)=0\), or linear function \(f(x)=x\). Then use transformations of this graph to graph the given function.
| 81. \(g( x ) = \sqrt [ 3 ] -1\) 82. \(g( x ) = \sqrt [ 3 ] < x - 1 >\) | 83. \(g( x ) = \sqrt [ 3 ] < x - 2 >+ 6\) 84. \(g( x ) = \sqrt [ 3 ] < x + 8 >- 4\) 84.1 \(g( x ) = \sqrt [ 3 ] < -x + 3 >- 2\) | 84.1 \(g( x ) = - \sqrt [ 3 ] < x - 1 >+ 2\) 85. \(g ( x ) = -2 \sqrt [ 3 ] < x + 3 >+ 4\) 86. \(g ( x ) = \sqrt [ 3 ] - 1\) | 87. \(f(x) = x + 3\) 88. \(h ( x ) = - 2 x + 1\) 89. \(g(x) = −4\) |
\( \bigstar\) Begin by graphing the basic reciprocal function \(f(x)=\frac\). State the transformations needed to apply to \(f\) to graph the function below. Then use transformations to graph the function.
| 91. \(f(x) = \dfrac\) 92. \(f(x) = \dfrac\) 93. \(f(x) = \dfrac + 5\) | 94. \(f(x) = \dfrac − 3\) 95. \(f(x) = \dfrac − 2\) 96. \(f(x) = \dfrac + 3\) | 97. \(f ( x ) = - \dfrac < 1 >< x + 2 >\) 98. \(f ( x ) = - \dfrac < 1 >< x >\) 99.\(p( x ) = - \dfrac < 1 > < x + 1 >+ 2\) | 100.1 \(a(x) = \dfrac -5 \) 100.2 \(b(x) = \dfrac +4 \) |
27. \(y = x^\); Shift up \(1\) unit; domain: \(ℝ\); range: \([1, ∞)\)  | 29. \(y = x^\); Shift right \(5\) units; domain: \(ℝ\); range: \([0, ∞)\)  | 31. \(y = x^\); Shift right \(5\) units and up \(2\) units; domain: \(ℝ\); range: \([2, ∞)\)  |
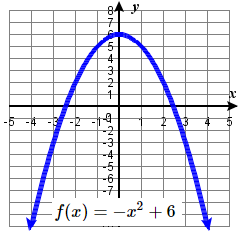
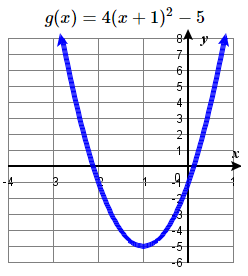
33. Shift left \(1\) unit and down \(3\) units;  \(f(t)=(t+1)^2−3\) | #35 Reflect over x-axis, up \(6\) units.  | 37 \(f(x)=x^2\) is shifted to the left \(1\) unit, stretched vertically by a factor of \(4\), and shifted down \(5\) units.  |
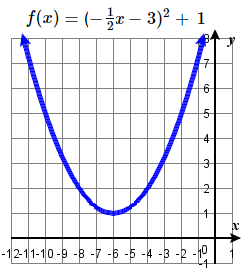
39. Shift right \(1\) unit, and vertically shrink by a factor of \( \frac\)  | #41 Shift right \(3\), reflect over \(y\)-axis, horizontally stretch by a factor of \(2\), up \(1\) units.  | for # 41, if \(f ( x ) = ( -\tfracx - 3 ) ^ 2 + 1\) is rewritten as \(f ( x ) = ( -\tfrac(x + 6) ) ^ 2 + 1\) , then the transformations would be horizontal stretch by a factor of 2, reflect in \(y\)-axis (no change), left 6, up 1. |
43. \(y = \sqrt\); Shift down \(5\) units; domain: \([0, ∞)\); range: \([−5, ∞)\) 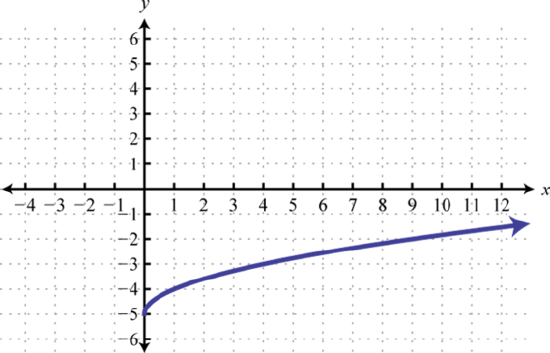 | 45. \(y = \sqrt\); Shift right \(2\) units and up \(1\) unit; domain: \([2, ∞)\); range: \([1, ∞)\) 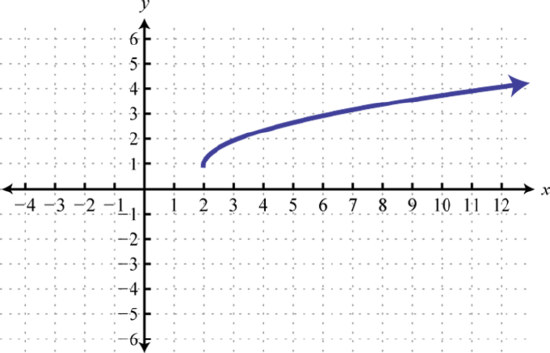 | 47 The graph of \(f(x)=\sqrt\) is shifted left \(4\) units and then reflected across the \(y\)-axis. 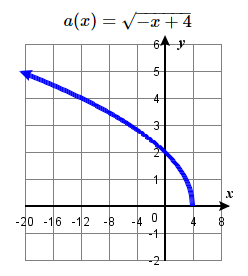 |
49. Reflect over \(y\)-axis, up \(2\) 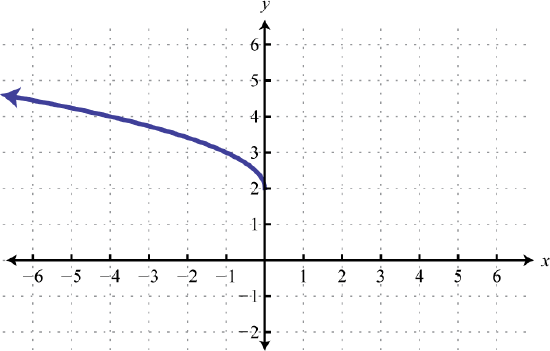 | 51. Right \(3\), Reflect over \(x\) axis, Vertically compressed by a factor of \(1/2\). 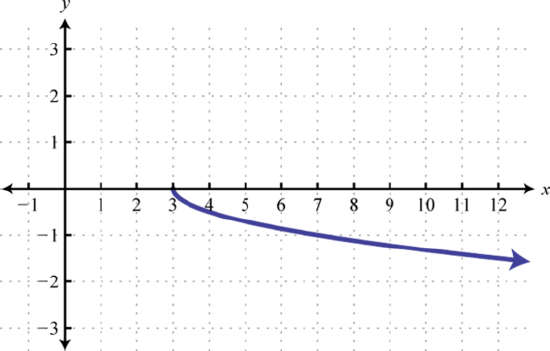 | 53. Right 1, Vertically stretched by a factor of \(4\), up \(2\) 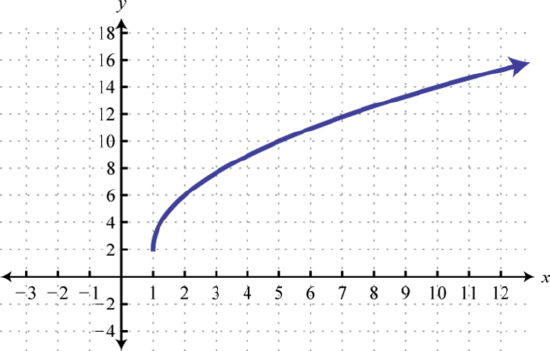 | #55 Horizontal compression by \(1/2\), shift left \(2.5\), down \(1\) unit. 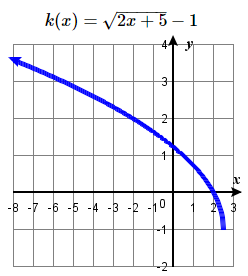 |
57. \(y = |x|\); Shift left \(4\) units; domain: \(ℝ\); range: \([0, ∞)\) 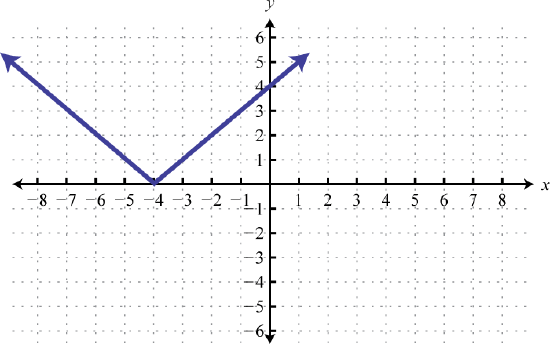 . . | 59. \(y = |x|\); Shift right \(1\) unit and down \(3\) units; domain: \(ℝ\); range: \([−3, ∞)\)  . . | 61. Right \(1\), Reflect over \(x\)-axis 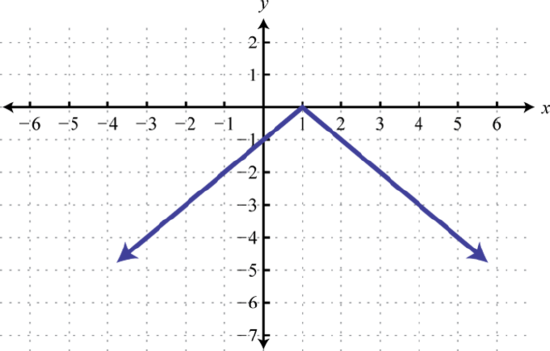 . . |
63. Reflect over \(x\)-axis, vertically stretch by a factor of \(3\) 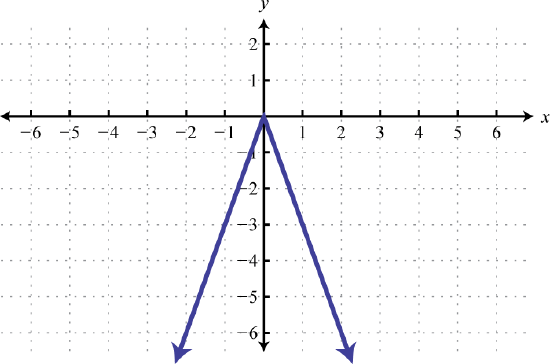 | 65 The graph of \(f(x)=|x|\) is shifted horizontally \(4\) units to the right, stretched vertically by a factor of \(2\), reflected across the horizontal axis, then shifted up \(3\) units. 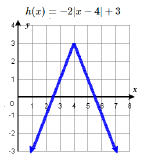 | 67. \(h(x) = |-3(x-\tfrac)| -2 \) \( \longrightarrow\) Horizontally compress by a factor of \(\tfrac\), right \( \tfrac\), down \(2\) 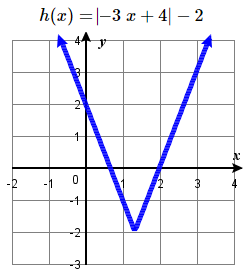 |
69. \(y = x^\) ; Shift right \(2\) units; domain: \(ℝ\); range: \(ℝ\) 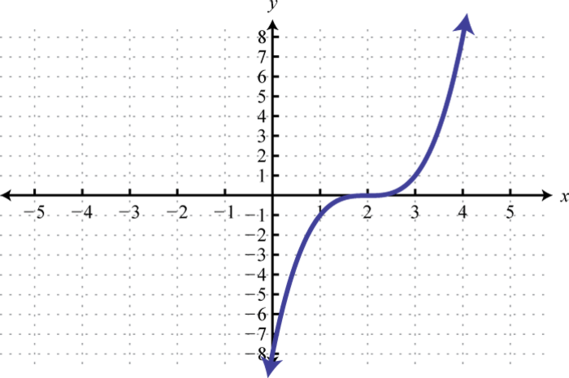 | 71. \(y = x^\); Shift right \(1\) unit and down \(4\) units; domain: \(ℝ\); range: \(ℝ\) 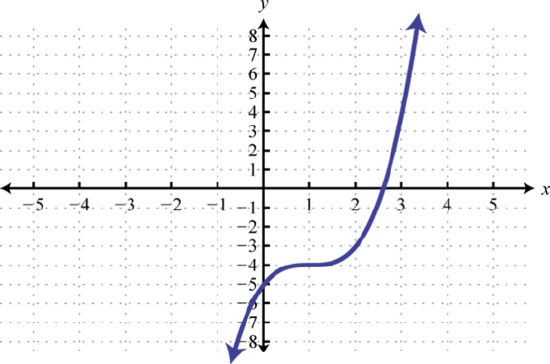 | 73. Left \(2\) units, reflect over x-axis 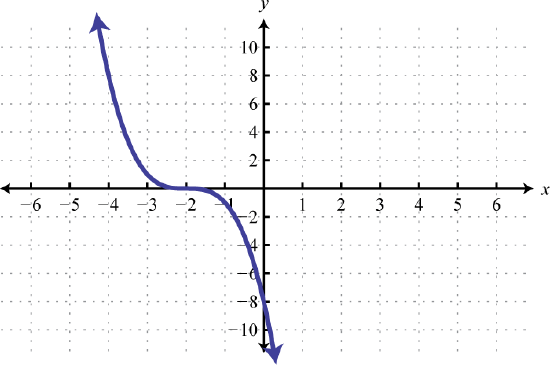 |
75. Reflect over x-axis, up \(4\) units 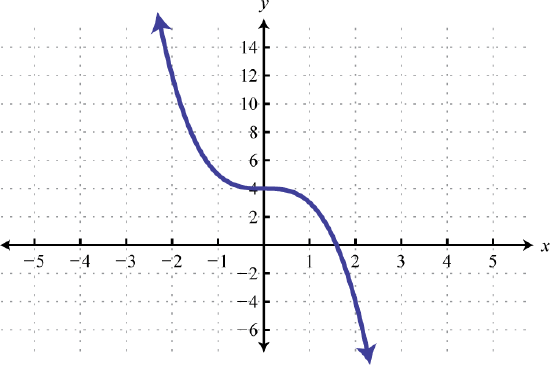 | 77. Left \(3\) units, reflect over x-axis, vertically shrink by a factor of \(\frac \), down \(1\) unit 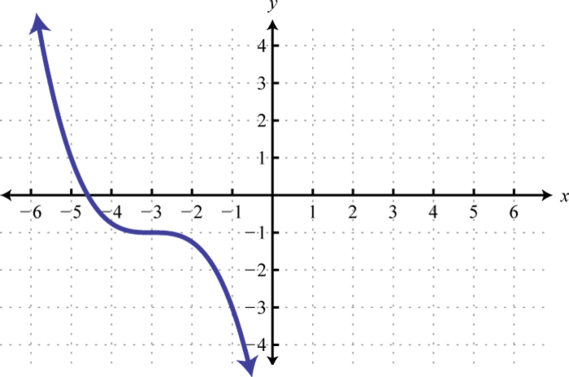 | 79. Stretch horizontally by a factor of \(3\) and shift vertically downward by \(3\) units. 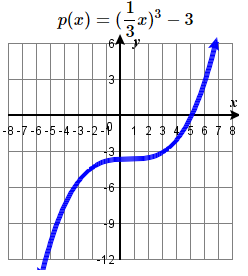 |
Answers to Odd Numbered Exercises for the Cube Root, Linear and Constant Functions Cube Root, Linear, Constant Functions
81. \(y = \sqrt [ 3 ] < x >\); Shift down \(1\) 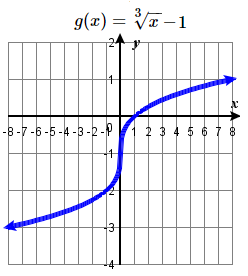 | 83. \(y = \sqrt [ 3 ] < x >\); Shift up \(6\) units and right \(2\) units; domain: \(ℝ\); range: \(ℝ\) 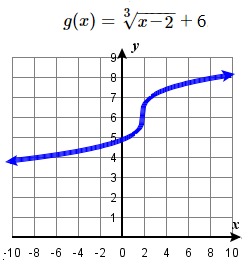 | 85. \(y = \sqrt [ 3 ] < x >\); Left \(3\), reflect over \(x\)-axis, vertically stretch by a factor of \(2\), up \(4\). 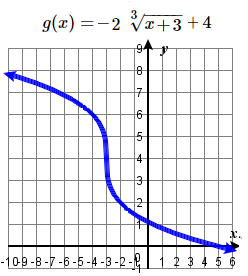 |
87. \(y = x\); Shift up \(3\) units; domain: \(\mathbb\); range: \(\mathbb\) 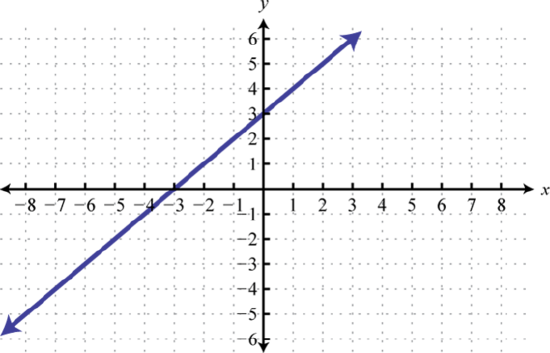 | 89. Basic graph \(y = −4\); domain: \(ℝ\); range: \(\\)  |
91. \(y = \frac\); Shift right \(2\) units; domain: \((−∞, 2) ∪ (2, ∞)\); range: \((−∞, 0) ∪ (0, ∞)\) 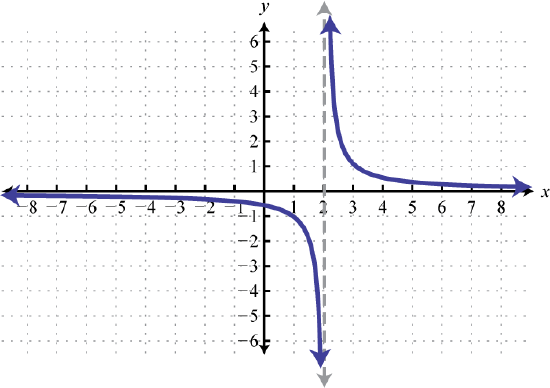 | 93. \(y = \frac\); Shift up \(5\) units; domain: \((−∞, 0) ∪ (0, ∞)\); range: \((−∞, 1) ∪ (1, ∞)\) 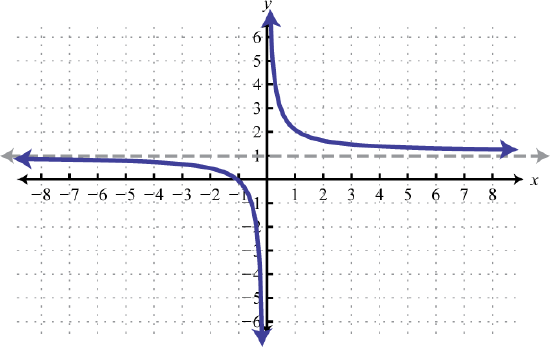 \( \star \) \( \star \) | 95. \(y = \frac\); Shift left \(1\) unit and down \(2\) units; domain: \((−∞, −1) ∪ (−1, ∞)\); range: \((−∞, −2) ∪ (−2, ∞)\) 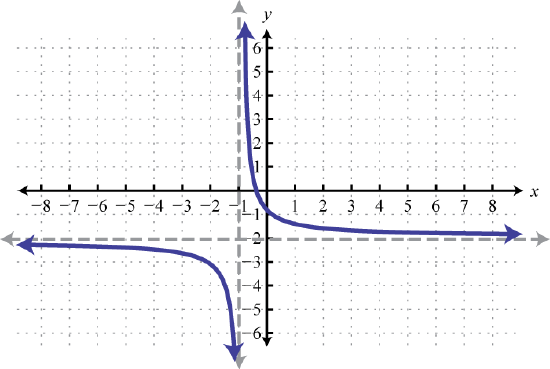 97 97 |
97. Left \(2\) units, reflect over x-axis 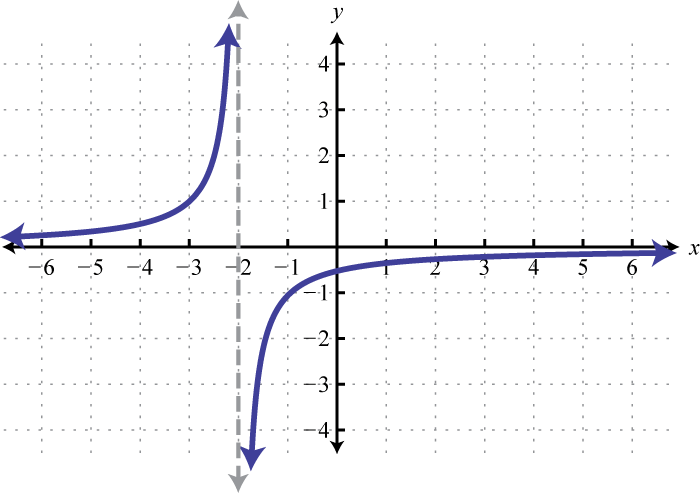 | #99 Left \(1\) unit, reflect over x-axis, up \(2\) units. 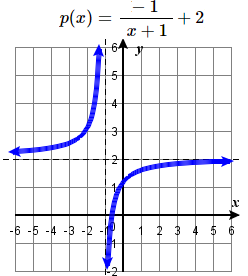 |
Exercise \(\PageIndex
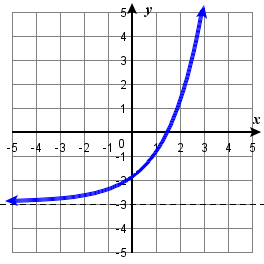
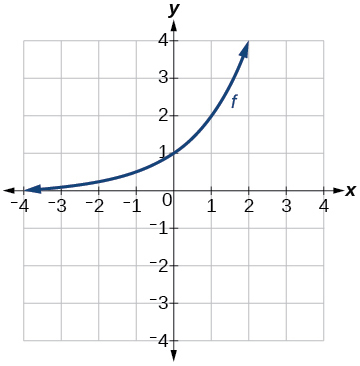 Given the graph of \(f(x)\) on the right, sketch the graph for the following transformations of \(f\) 101. \(h(x)=2^x-3\) 102. a) \(g(x)=2^x+1\) b) \(w(x)=2^x−1\) Given the graph of \(f(x)\) on the right, sketch the graph for the following transformations of \(f\) 101. \(h(x)=2^x-3\) 102. a) \(g(x)=2^x+1\) b) \(w(x)=2^x−1\) | 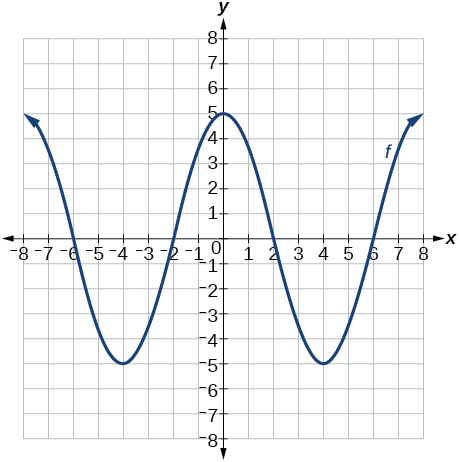 Given the graph of \(f(x)\) on the right, sketch the graph for the following transformations of \(f\) 103. a) \(g(x)=−f(x)\) b) \(g(x)=f(x−2)\) 104. a) \(g(x)=f(x)−2\) b) \(g(x)=f(x+1)\) Given the graph of \(f(x)\) on the right, sketch the graph for the following transformations of \(f\) 103. a) \(g(x)=−f(x)\) b) \(g(x)=f(x−2)\) 104. a) \(g(x)=f(x)−2\) b) \(g(x)=f(x+1)\) |
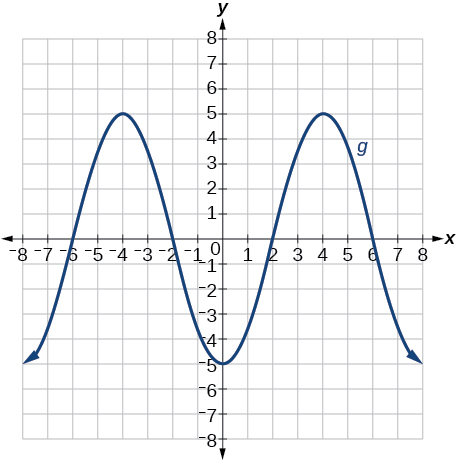
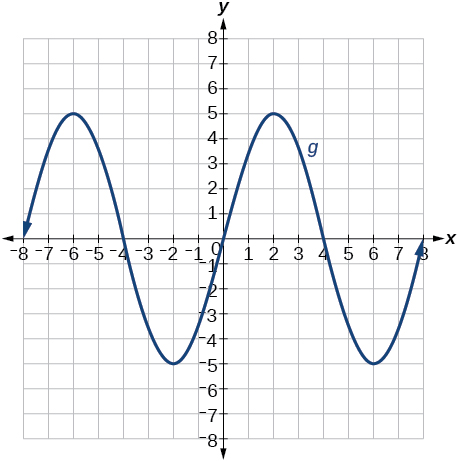
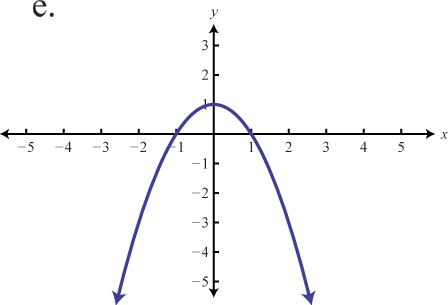
\( \bigstar\) Match the graph to the function definition.
108. \(f(x) = |x − 2| − 2\)
110. \(f(x) = |x − 2| + 1\)
112. \(f(x) = |x + 2| − 2\)
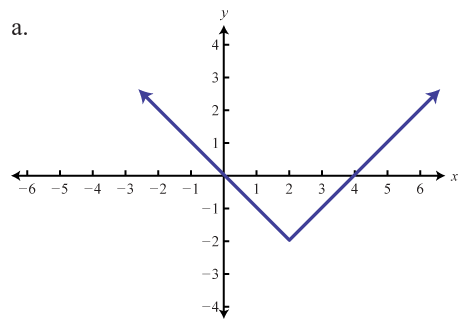
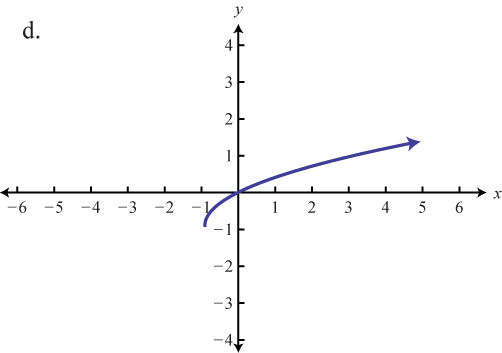
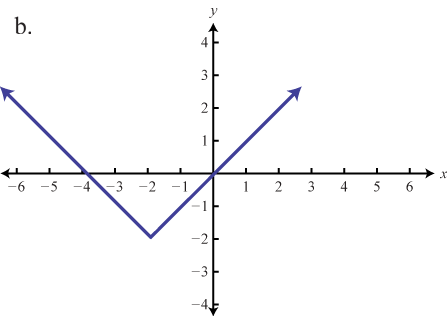
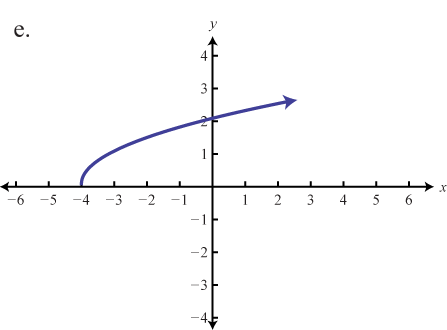
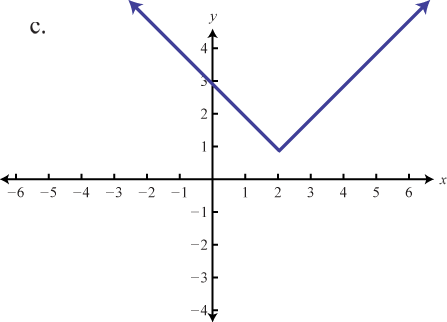
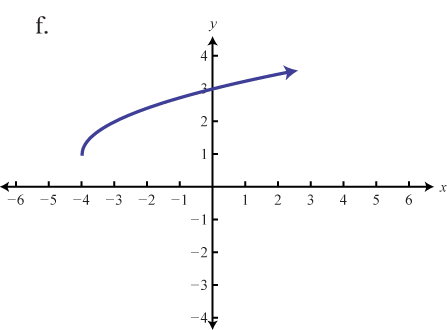
Match the graph to the given function definition.
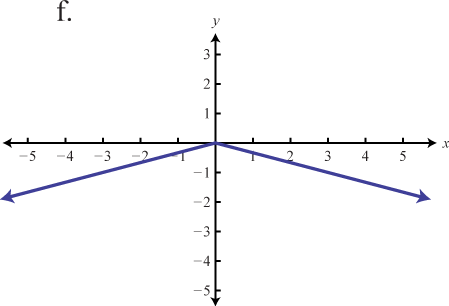
113. \(f ( x ) = - 3 | x |\)
114. \(f ( x ) = - ( x + 3 ) ^ < 2 >- 1\)
115. \(f ( x ) = - | x + 1 | + 2\)
116. \(f ( x ) = - x ^ < 2 >+ 1\)
117. \(f ( x ) = - \frac < 1 > < 3 >| x |\)
118. \(f ( x ) = - ( x - 2 ) ^ < 2 >+ 2\)
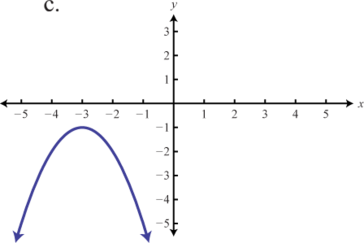
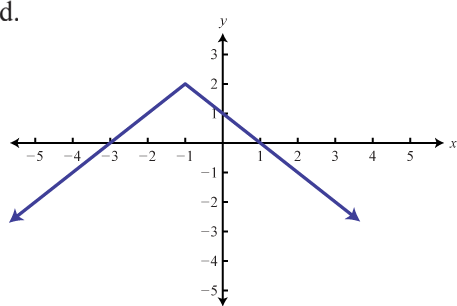
part 1 answers 107e, 109d, 111f, part 2 Answers: 113.b, 115.d, 117.f
\( \bigstar\) Write an equation for each graphed function by using transformations of the graphs of one of the toolkit functions.
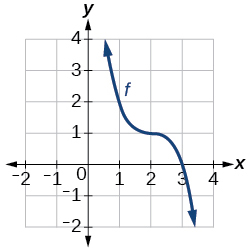
130. (a)
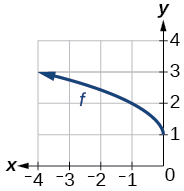
130. (b)
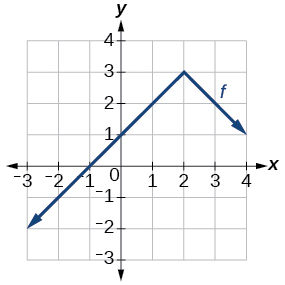
| 119. \(f(x)=|x-3|−2\) 121. \(f(x)=\sqrt−1\) | 123. \(f(x)=(x-2)^2\) 125. \(f(x)=|x+3|−2\) | 127. \(f(x)=−\sqrt\) 129. \(f(x)=−(x+1)^2+2\) |
\( \bigstar\) Write an equation that represents the function whose graph is given.
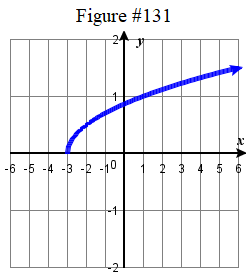
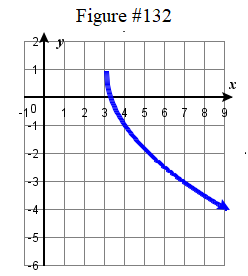
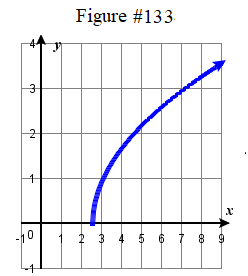
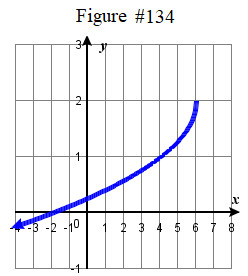
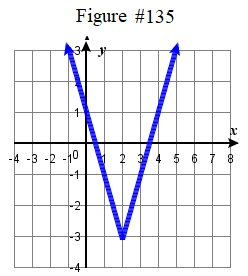
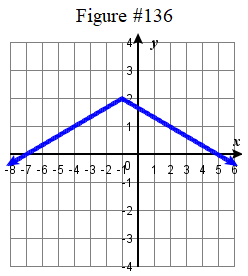
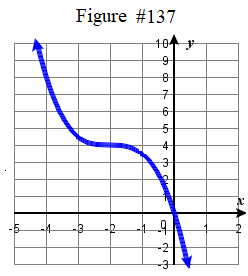
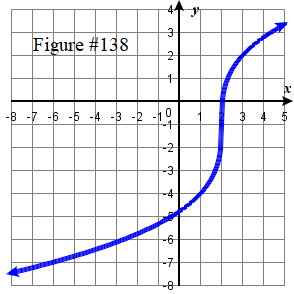
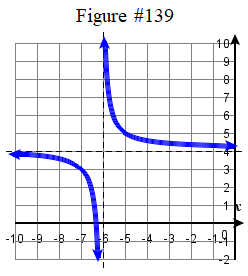
| 131. \(f ( x ) = \tfrac \sqrt < x +3 >\) | 133. \(f ( x ) = \sqrt(2x-5) \) 135. \(f ( x ) = 2 | x-2 | - 3\) | 137. \(f ( x ) = -\tfrac ( x + 2 )^3 +4\) | 139. \( f(x) = \dfrac + 4\) |
\( \bigstar\) Write a formula for the function with the following transformations
141. Write a formula for the function obtained when the graph of \(f(x)=|x|\) is shifted down \(3\) units and right \(1\) unit.
142. Write a formula for the function obtained when the graph of \(f(x)=\dfrac\) is shifted down \(4\) units and right \(3\) units.
143. Write a formula for the function obtained when the graph of \(f(x)=\dfrac\) is shifted up \(2\) units and left \(4\) units.
144. Write a formula for the function obtained when the graph of \(f(x)=\sqrt\) is shifted up \(1\) unit and left \(2\) units.
145. The graph of \(f(x)=|x|\) is reflected over the \(y\)-axis and horizontally compressed by a factor of \(\dfrac\).
146. The graph of \(f(x)=\sqrt\) is reflected over the \(x\)-axis and horizontally stretched by a factor of \(2\).
147. The graph of \(f(x)=\dfrac\) is vertically compressed by a factor of \(\dfrac\), then shifted left \(2\) units and down \(3\) units.
148. The graph of \(f(x)=\dfrac\) is vertically stretched by a factor of \(8\), then shifted to the right \(4\) units and up \(2\) units.
149. The graph of \(f(x)=x^2\) is vertically compressed by a factor of \(\dfrac\), then shifted to the right \(5\) units and up \(1\) unit.
150. The graph of \(f(x)=x^2\) is horizontally stretched by a factor of \(3\), then shifted left \(4\) units and down \(3\) units.
Answers to Odd Exercises: